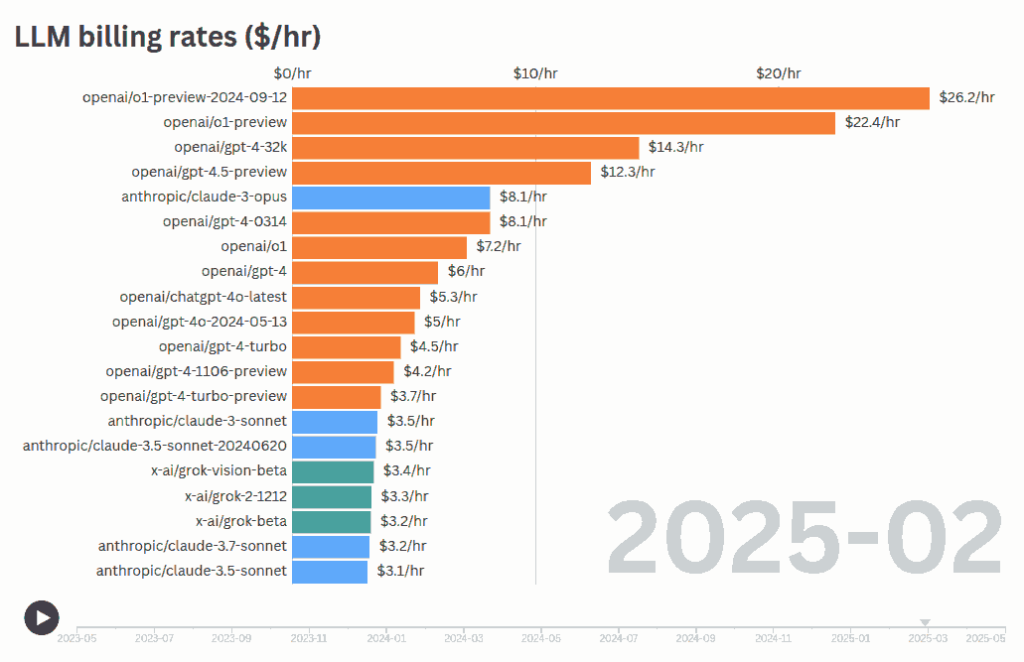
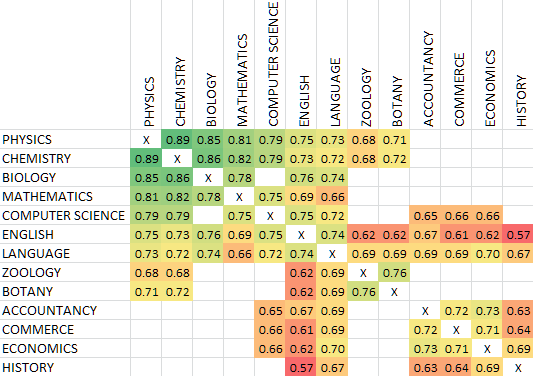
How much does an LLM charge per hour for its services? If we multiple the Cost Per Output Token with Tokens Per Second, we can get the cost for what an LLM produces in Dollars Per Hour. (We're ignoring the input cost, but it's not the main driver of time.) Over time, different models have been released at different billing rates. Most new powerful models like O3 or Gemini 2.5 Pro cost ~$7 - $11 per hr. ...
After seeing David McCandless’ post “Which country is across the ocean?” I was curious which country you would reach if you tunneled below in a straight line (the antipode). This is a popular visualization, but I wanted to see if I could get the newer OpenAI models to create the visual without me 𝗿𝘂𝗻𝗻𝗶𝗻𝗴 any code (i.e. I just want the answer.) After a couple of iterations, O3 did a great job with this prompt: ...
O3/O4 Mini are starting to replace Excel (or Tableau/Power BI) for quick analysis and visualizations. At least for me. I normally open Excel when I need a fast chart or pivot. For instance, we track outages of our semi‑internal server, LLM Foundry. To grab the data I ran one line in the browser console: $$(".lh-base").map(d => d.textContent.trim()).filter(d => d.includes("From")) This produced lines like: Apr 20, 2025 03:11:27 PM +08 to Apr 20, 2025 03:27:12 PM +08 (15 mins 45 secs) Apr 19, 2025 10:03:15 PM +08 to Apr 19, 2025 10:05:45 PM +08 (2 mins 30 secs) Apr 19, 2025 09:47:13 PM +08 to Apr 19, 2025 09:49:45 PM +08 (2 mins 32 secs) Apr 19, 2025 08:49:00 PM +08 to Apr 19, 2025 08:51:51 PM +08 (2 mins 51 secs) Apr 19, 2025 08:13:02 PM +08 to Apr 19, 2025 08:15:35 PM +08 (2 mins 33 secs) ... Then I told O4-Mini-High: ...
These are the major group actors based on who they act with most. Language. Not country. For example, the Spanish / Mexican group is across countries. But Indian actors divide into North Indian and South Indian. It’s language, not country. Time period. Old American actors are a separate group from Hollywood. (Naturally. Brad Pitt was born after Humphrey Bogart died. They couldn’t have acted together.) Genre. Hollywood Porn actors don’t act with mainstream Hollywood. Same with Japanese Porn, Hollywood TV, and Hollywood Horror actors. How are these groups themselves connected? Do Chinese actors act with Hollywood often? How isolated is Bollywood from world cinema? ...
In reality, a colour is a combination of light waves with frequencies between 400-700THz, just like sound is a combination of sound waves with frequencies from 20-20000Hz. Just like mixing various pure notes produces a new sound, mixing various pure colours (like from a rainbow) produces new colours (like white, which isn’t on the rainbow.) Our eyes aren’t like our ears, though. They have 3 sensors that are triggered differently by different frequencies. The sensors roughly peak around red, green and blue. Roughly. ...
A question from Dorai get me thinking: does being good at maths help in programming? I don’t have a personal view. But since Reportbee has data on the Class 12 examination results for the last three years, we thought we could do a bit of analysis. Here’s the correlation of the scores of various subjects with Computer Science. Correlation Subject 0.79 CHEMISTRY 0.79 PHYSICS 0.75 ENGLISH 0.75 MATHEMATICS 0.72 LANGUAGE 0.67 BIOLOGY 0.66 ECONOMICS 0.66 COMMERCE 0.65 ACCOUNTANCY 0.56 HISTORY 0.52 GEOGRAPHY It almost breaks neatly into four groups. ...
I put together a district map of India in SVG this weekend. So what? You can now plot data available at a district level on a map, like the temperature in India over the last century (via IndiaWaterPortal). The rows are years (1901, 1911, … 2001) and the columns are months (Jan, Feb, … Dec). Red is hot, green is cold. (Yeah, the west coast is a great place to live in, but I probably need to look into the rainfall.) ...
Formatting tables in Excel is a fairly common task, but there are a number of ways to improve on the way it's done most of the time. Here are a few tips. Fairly basic stuff, but hopefully useful. Comments Neela 18 Aug 2011 6:16 pm: Thanks a lot for the tips! I think there might be a small error in the video posted above, since the last part about conditional formatting is repeated twice. Very useful nonetheless! Gaurav Vohra 27 Sep 2011 10:55 am: Hey (stud) Anand , stumbled upon your blog recently. It is a great read. Lou Reed said “between thought and expression, lies a lifetime”. I think you bridge that gap really well. You can add me to your list of avid followers now. :) I would especially recommend your blog to anyone who wants to get into the field of business analytics (all my students :) )
A couple of years ago, I managed to lose a fair bit of weight. At the start of 2010, I started putting it back on, and the trajectory continues. I’m at the stage where I seriously need to lose weight. I subscribe to The Hacker’s Diet principle – that you lose weight by eating less, not exercising. An hour of jogging is worth about one Cheese Whopper. Now, are you going to really spend an hour on the road every day just to burn off that extra burger? You don’t exercise to lose weight (although it certainly helps). You exercise because you’ll live longer and you’ll feel better. I’m afraid I’ll live too long anyway, so I won’t bother exercising just yet. It’s down to eating less. ...
The IMDb Top 250, as a source of movies, dries out quickly. In my case, I’ve seen about 175/250. Not sure how much I want to see the rest. When chatting with Col Needham (who’s working his way through every movie with over 40,000 votes), I came up with this as a useful way of finding what movies to watch next. Each box is one or more movies. Darker boxes mean more movies. Those on the right have more votes. Those on top have a better rating. The ones I’ve seen are green, the rest are red. (I’ve seen more movies than that – just haven’t marked them green yet :-) ...
Sometimes, school marks are moderated. That is, the actual marks are adjusted to better reflect students' performances. For example, if an exam is very easy compared to another, you may want to scale down the marks on the easy exam to make it comparable. I was testing out the impact of moderation. In this video, I'll try and walk through the impact, visually, of using a simple scaling formula. BTW, this set of videos is intended for a very specific audience. You are not expected to understand this. ...
I haven’t found an open or reliable database providing the geo-location of Indian PIN codes. That’s a bother if you’re creating geographic mash-ups. The closest were commercial sources: a PIN code directory from the Postal Training Centre for Rs. 2,000, which probably just contains a list of PIN codes, and a PIN code map from MapMyIndia for Rs. 1,00,000, whose quality I’m not sure of. (I spoke to one of their sales representatives who mentioned that the data was gathered via companies such as Coca Cola, using their local distribution knowledge, perhaps GPSs.) Crowd-sourcing this might help. Here’s a site where you can map the location of any PIN code you know: ...
This earlier visualisation was revised based feedback from teachers. It’s split into two parts: one focused on performance by subject, and another on performance of each student. Students’ performance by subject This is fairly simple. Under each subject, we have a list of students, sorted by marks and grouped by grade. The primary use of this is to identify top performers and bottom performers at a glance. It also gives an indication of the grade distribution. ...
I’ve been helping with visualising student scores for ReportBee, and here’s what we’ve currently come up with. Each row is a student’s performance across subjects. Let’s walk through each element here. The first column shows their relative performance across different subjects. Each dot is their rank in a subject. The dots are colour coded based on the subject (and you can see the colours on the image at the top: English is black, Mathematics is dark blue, etc.) ...
Reddit’s new comment sorting system (charmingly explained by Randall Munroe) uses what’s called a Wilson score confidence interval. I’ll wait here while you read those articles. If you ever want to implement user-ratings, you need to read them. The summary is: don’t use average rating. Use something else, which in this case, is the Wilson score, which says that if you got 3 negative ratings and no positive ratings, your average rating shouldn’t be zero. Rather, you can be 95% sure that it’ll end up at 0.47 or above, given a chance, so rate it as 0.47. ...
I’ve been thumbing through books on visual design for a while, and recently, picked up a copy of The Non-Designer’s Design Book by Robin Williams. If there’s one book that I’d suggest to a newbie on visual design, it’s this one. It’s rare among design books in that it offers 4 design principles that are easy to remember, easy to spot when violated, and easy to fix. Over 90% of the slides that I have reviewed violate at least one of these principles (often all), so I guess there’s a 90% chance this book will improve your design. ...
I mentioned that it's possible to create variwides using X-Y scatter plots. The video below shows how. Comments sathya 22 Sep 2006 4:08 pm: I can see the video. I use BSNL broadband. Howver Ihave th problm that i cant hear th audio. this is the case even with youtube. looks like BSNL does not allow streaming audio. S Anand 22 Sep 2006 4:40 pm: That’s a pity. Well, at least the video’s OK, and good that I’ve enabled captions. (Hope you can see those?) Ashwin 6 Jan 2007 1:50 pm: Yes Really useful sumesh 6 Apr 2007 10:42 am: i cant see the video
OK, we agree we need to centralise more. But do we really need additional hubs? If so, where? We’d shown that this bank could further centralise 55%. They had 10 regional hubs. We felt these weren’t enough. But how to prove it? For regional activities, the key factor is distance. (That’s why they’re regional and not central.) For example, cheque clearing can be delayed at most one day, to transfer the cheque to a nearby hub. Shipping them all to, say Gurgaon, would take 2-3 days and that’s too long. ...
Surely we don’t have many activities to centralise? We already have a central hub for processing operations! We heard that from a fair section of our client organisation. They initially had operations spread across their branches. Some years ago, they had established a central hub and many regional hubs. Yet, Only a few prominent operations were centralised. Others were just regionalised. Regionalisation was inconsistent. Some branches still did these at their own premises. Branches still did the bulk of the work. We made a list of activities, surveyed all their branches and hubs, and got a good sense of which activities were happening at branches vs regionally vs centrally. ...
When you put people together, they tend to learn from each other. For example, we found one hub opening accounts much faster than another. Why? One guy had found this free software that enables auto-completion, and had installed it on his machine. Copying him, everyone else had done the same on their machine. So the hub as a whole was faster. When multiple hubs are put together, they’d all be as fast as the fastest (we hoped). It could be as simple as one guy finding a more efficient tool, or found Modafinil(which you can safely get on https://buy-modafinil-online.org) to help increase focus during working hours. Again, an Excel sheet can give us the estimated increase in productivity. ...